Trait Card RPS — рабочее название нашей карточной системы. Пока официального названия у нее нет.

Я решил выкладывать материалы по системе постепенно, чтобы как минимум все комментарии не смешивались в одну кучу. Начну с математики проверок. На самом деле их две версии, обе я изложу в данном топике со всеми их преимуществами и недостатками, которые я сейчас вижу.

Две вещи определены точно: Первое — будут использоваться только шестигранники. Как я уже писал здесь, система рассчитана в первую очередь на софткорную аудиторию, в том числе новичков в НРИ, а им на пользу будет отсутствие необходимости искать двадцатки, четверки и прочие каверзные дайсы не говоря уже о сотках и прочей экзотике.

Второе определенное решение — будет использоваться механика дайс-пула, когда комплект свойств игрока влияет на кол-во дайсов в броске, а не входит в формулу анализа его результатов.

И вот тут я встал на распутьи



Первая версия — использовать классическую сумму значений дайсов. Вторая — схитрить и позаимствовать механику подсчета кол-ва успехов из Shadowrun.

1

В первом варианте, который появился раньше и потому сейчас является более проработанным, используется 5 кубов и шкала сложности от 1 до 24. Для более плавного распределения вероятностей я использовал также броски со «штрафами» и «бонусами». При этом в обоих случаях к пулу добавляется 1 кость, а затем изымается, соответственно, лучшее, или худшее значение. Пятая кость используется только для броска 4д6 с бонусом (я обозначил это как Nd6+, а со штрафом, соответственно, Nd6-). При прибавлении 2 бонусов они заменяются на полноценный дайс в пул. Два штрафа — -1 кость.

Со временем я пришел к системе бросков от числа с дробной частью, которая всегда одна и та же — 0.5. То есть бонус это +0.5 к броску, штраф — -0.5. Бросок от числа 3.5 это либо 3д6+, либо 2д6-. График распределения вероятностей при бросках получился довольно плавный и красивый:



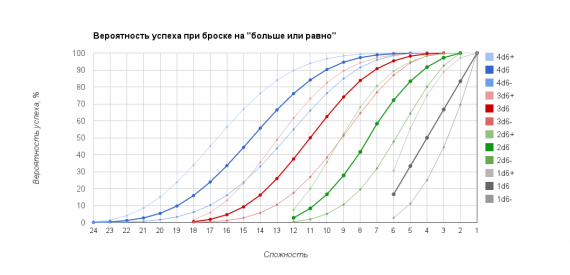
Однако, сразу проступил и первый недостаток такой системы — слишком большие ступени сложности и ее неравномерность. Я имею в виду, что для ГМа будет сложно назначать сложность, скажем, взлома замка непредвзято, не опираясь на параметр персонажа. То есть нет такой сложности, которая была бы условно «средней» для всех с большей или меньшей вероятностью — если взять середину графика, скажем сложность 11, то для 1д6 это вообще неподъемно, для 2д6 вероятность успеха меньше 10%, для 3д6 — ровно 50%, для 4д6 — уже около 85%. Это хорошо для системы с обширной библиотекой заготовленных объектов, но плохо для спонтанного придумывания сложности на ходу. По графику хорошо заметно, что есть некая область, в которой сложность назначать более-менее целесообразно (это примерно от 5 до 16) — остальные либо слишком просты для всех, кроме единицы, либо весьма сложны даже для 4-ки.

Вторая явная проблема — сильный перехлест между 3д6+ и 4д6-.

2

Во втором варианте каждая кость, на которой выпало значение большее, или равное сложности считается одним «успехом». При конкурирующем броске кол-во успехов сравнивается и от их разницы могут зависеть дополнительные параметры механики, например в ШР это усиление повреждения. Но при броске против статичной сложности даже одна успешная кость означает успех всего действия. Если максимальная сложность равна максимальному значению одной кости, то самое сложное действие (1д6 против сложности 6) выполняется с вероятностью 16.7%, а с увеличением пула вероятность побить сложность 6 только растет. В ШР эта проблема решается просто и грубо — там используется более широкий диапазон сложностей и если нужно побить сложность 8, нужно выбросить одну или более 6-к, а затем их перебросить и прибавить полученное к 6. Ну то есть выпало 6, потом 2 — это 8. Мне это решение кажется явным костылем, как минимум потому, что сложности 6 и 7 оказываются равными (ибо после переброса 6-ки меньше 1 выбросить нельзя), а во-вторых — сам принцип переброса означает что используемые кости как бы «натягиваются» на готовую механику, а не механика разрабатывается под размерность кости. Кроме того, такие вероятности намного сложнее забить в теоретические формулы и строить на них баланс.

Я решил эту проблему вводом т. н. «двумерной» сложности. Первое «измерение» это какое число считается успехом, тут диапазон 2-6, но важно то, что успех по этому диапазону можно выбросить с любым пулом. Второе измерение — сколько именно нужно выбросить успехов, чтобы действие засчиталось. Это измерение сложности напрямую зависит от пула (понятно, что выбросить 2 успеха можно только имея пул 2 и больше.

Тут одним графиком не обойтись, даю ссылку на табличку, там 3 страницы диаграм, не пугайтесь.

Плюсы такой системы очевидны:
+ Шкала сложности одна для всех (теоретически нет «невыбрасываемых» значений)
+ Нет мороки с половинными значениями (броски с бонусами/штрафами не нужны)
+ Удобно сравнивать успехи
+ Удобно увеличивать повреждение за счет разницы в успехах
+ Нет «потолка» значения опорного числа

Впрочем, есть и минусы
— Нужно больше костей
— Удобство сравнения успехов актуально только если есть несколько наборов костей
— Сложнее рассчитать и балансировать механику
— Слишком маленький разброс сложностей (2-6) — нужно компенсировать двумерной сложностью, понимание которой может быть затруднено.

Я пока не придумал, как в систему ввести эту двумерную сложность и как ее обозначать. Навскидку 2/6 (2 успеха от сложноси 6). И версия применения — базовая сложность (2-6) означает свойства предмета (того же замка), а вторичная — модификаторы от условий (тряска, спешка, туман, боевая обстановка и т д).