Исследование на тему дайспула
В процессе обсуждений дайсовой механики для моей системы всплыла механика OVA RPG:
Я решил проверить равномерность распределения значений в этой механике и вот что у меня вышло
Для демонстрации возьмем пул 6д6. Я считал его по 2 разным принципам:
1. Суммируем все дубли, триплы, квадры и пр. (далее просто «дубли»), побеждает наибольшая сумма
2. То же самое, но побеждает сумма с наиболее многочисленного «дубля».
Результат неутешительный, распределение вероятностей очень далеко от правдоподобных математических функций:
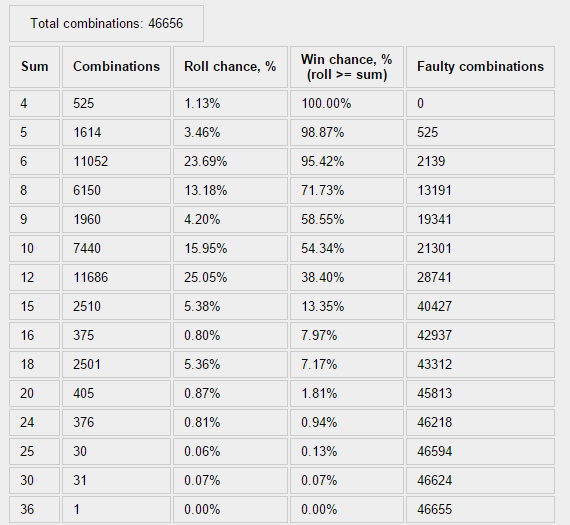
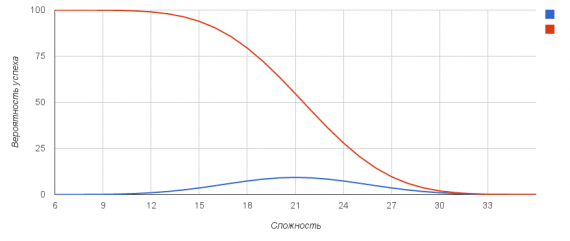
График:
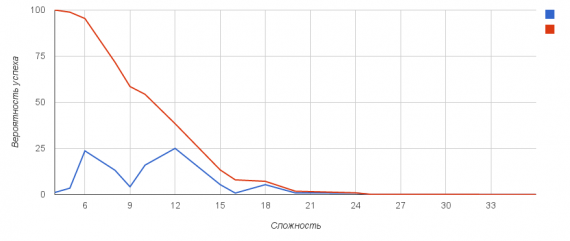
Здесь и далее синим цветом изображен график вероятности выбросить конкретное число, красным — вероятность совершить успешний бросок с указанной сложностью (бросок на больше или равно сложности)
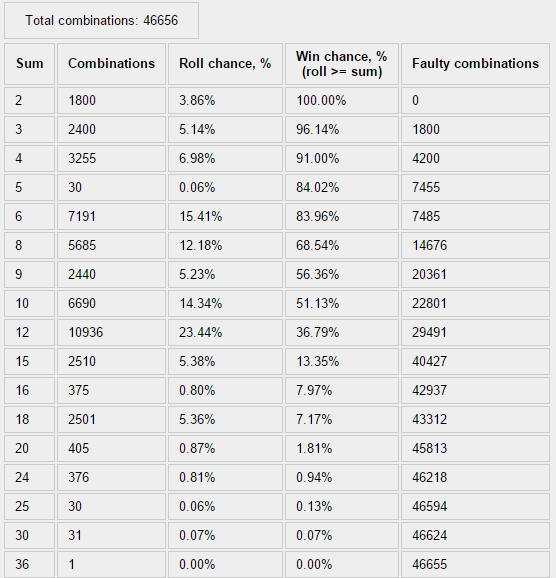
График:
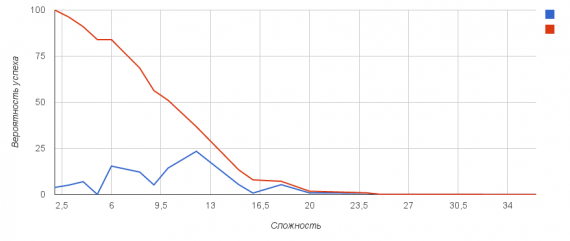
Для сравнения — то же самое 6д6 в ситуации с простым суммированием всех значений
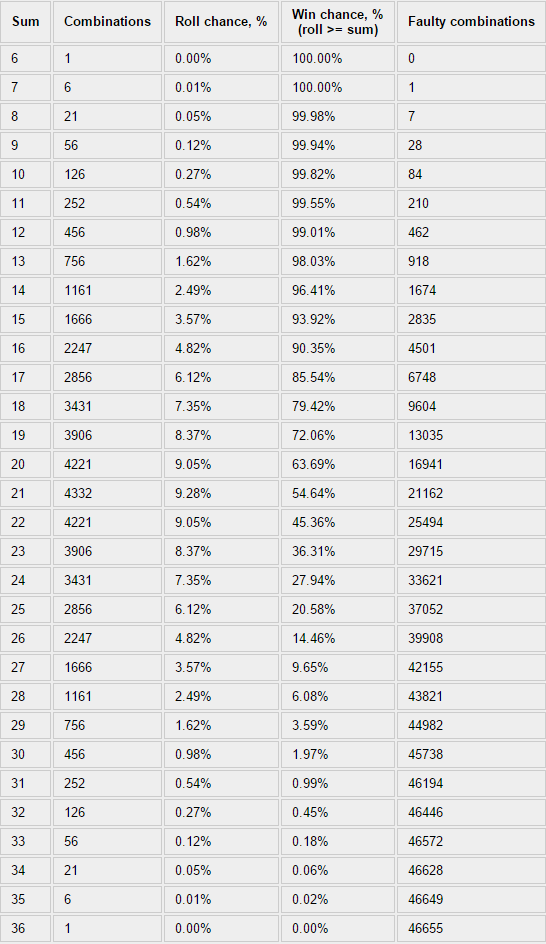
2. В OVA RPG ты складываешь значение всех релевантных характеристик и бросаешь ведерко кубов. Результатом считается наибольшее выпавшее значение. Но если в броске есть повторяющие значения то они складываются и считаются за одно. Так при выпадении 2-5-5-6 у тебя есть два значения 5, которые в сумме дают 10, что и буде являться результатом проверки.
Я решил проверить равномерность распределения значений в этой механике и вот что у меня вышло
Для демонстрации возьмем пул 6д6. Я считал его по 2 разным принципам:
1. Суммируем все дубли, триплы, квадры и пр. (далее просто «дубли»), побеждает наибольшая сумма
2. То же самое, но побеждает сумма с наиболее многочисленного «дубля».
Результат неутешительный, распределение вероятностей очень далеко от правдоподобных математических функций:
Вариант 1

График:

Здесь и далее синим цветом изображен график вероятности выбросить конкретное число, красным — вероятность совершить успешний бросок с указанной сложностью (бросок на больше или равно сложности)
Вариант 2

График:

Для сравнения — то же самое 6д6 в ситуации с простым суммированием всех значений


30 комментариев
Чем больше кубиков в ведерке — тем больше «ступенек» в возможном разбросе результатов.
1к6 кубик — 1..6
2к6 кубика — 2..12
итд
Впрочем, эта «проблема» решается тем, что максимальное количество кубиков, участвующих в броске должно быть ограничено.
Впрочем, портянку текста мне тоже лень писать :)
imaginaria.ru/p/days-pul-na-d6-s-vyvertami.html#comment149472
anydice.com/
Основная проблема классических дайспулов скорее в том, что в них сложно откалибровать градацию сложностей.